运动副间隙对高速精密压力机振动的影响

文：吴洋洋 ，赵 宇 ，吴洪涛 ，柯尊忙

摘要：曲柄压力机高速化带来振动加剧问题，影响工件质量、模具和机床的使用寿命。为研究间隙对压力机振动的影响，以JF75G一200型曲柄压力机为例，在RecurDyn中建立曲柄滑块机构的刚柔耦合动力学模型。在理想模型的基础上，加人了接触碰撞模型，探讨运动副间隙对压力机激振力大小的影响。并通过RecurDyn与Matlab联合仿真，分析了间隙对振幅大小的影响，从而为高速压力机的动平衡设计提供参考。

关键词：动力学仿真；高速精密压力机；运动副间隙；RecurDyn

随着现代科技的飞速发展和市场竞争的加剧，工业装备正向高速度、高精度、高柔性、多样化方向发展，锻压机械作为工业基础装备的重要组成部分之一，随着转速的不断提高，由此带来的振动和噪声明显加大，严重影响其机械性能和生产条件，因此，研究高精度、低噪声的高速精密压力机具有重要的现实意义。

机床的间隙在外界激励作用下使不同零部件之间产生碰撞振动，从而对系统的动力特性、可靠性和寿命等技术指标产生重要影响。曾梁彬」提出了一种基于动态响应的综合优化模型，通过有限元动态响应方法构造了一个直接以机身振动响应为对象的综合平衡优化模型，探讨了理想运动副情况一下压力机的动平衡计算。郭鹏飞」利用Monte Carlo方法对含间隙机构运动进行了概率分析，研究了间隙内碰撞和杆长误差对机构输出运动的影响。卢绪祥团基于广义Hertz接触理论，建立了含对称间隙结构的碰撞振动动力学模型，探讨了该模型的振动特性。

目前对于压力机的动平衡及机身振动的计算分析都是基于理想运动副，而运动副间隙的存在对振动的影响并未被考虑。本文采用多体系统动力学建立高速压力机传动系统模型，研究间隙对高速压力机振动的影响。

理想的旋转铰约束假定轴与轴套完全同心，为实现含间隙的旋转副和圆柱副，本文采用Recurl)yn 中相对坐标系的多体动力学接触分析算法。间隙碰撞模型简图如图1所示，它将孔的圆柱面近似为三角形碎片（称防御体），作为轴的圆柱面用一组球（称撞击体）表示，其中碎片和球的数量由计算精度决定。通过计算分析碎片和球之间是否接触，来判断两圆柱面是否碰撞，进一步确定旋转副和圆柱副所处的状态；若发生碰撞，则根据碎片和球之间的侵人量来确定穿深量。

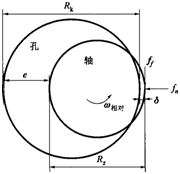
图1含间隙旋转副模型

图1中，为法向接触碰撞力，为切向摩擦力，e为间隙大小，Rk为孔的直径，Rz为轴的直径。对含间隙旋转铰，间隙大小用轴承与轴半径之差来描述，则间隙为：

（1）

先创建两个圆柱面的Extended Surface to Surface约束，再通过调整两圆柱面的直径，建立含间隙的旋转副和圆柱副模型。通过改变孔或者轴的偏差来调整间隙的大小。

RecurDyn中的间隙非线性连续接触碰撞力模型，其法向接触力计算公式为：

（2）

式中：K为接触刚度系数；和分别表示穿透深度及接触点的相对速度；c为阻尼系数；、2、 ” 3分别为刚度指数、阻尼指数及凹痕指数。这蚱参数取决于材料的类型、尺寸等，一般在默认值的基础上进行适当修改。接触刚度系数K根据Hertz碰撞理论中的等效刚度系数确定，计算公式为：

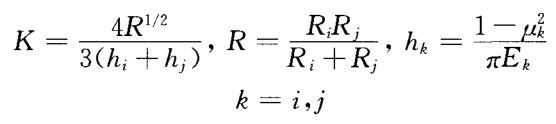（3）

式中：分别代表构件 i(j)在碰撞点处的曲率半径、材料的泊松比和弹性模量 。
通过切向摩擦力模 型来描述运动副间隙切 向接触特性 ，最为著名的摩擦力模型是 Coulomb 摩擦模型，该模型通常用于描述冲击或接触碰撞过程中的摩擦行为。本文采用修正的 Coulomb 摩擦力模型，该模型在 Coulomb 摩擦模型基础上提出了动态摩擦系数的概念 ，摩擦 系数不是一个 常数 ，而是切 向滑动速度的函数 ，切向摩擦力计算公式为：
（4）

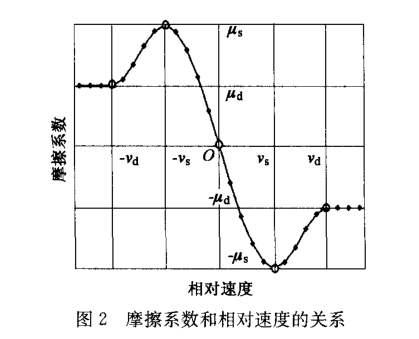
式中：μ (v ) 是摩擦系数，其符号和数值 由接触位置和接触两者的相对速度决定，与相对速度的关系如图2 所示。当相对速度的绝对值小于静态门槛速Vs时，摩擦系数在-Vs~Vs之间插值；当相对速度的绝对值介于静态门槛速度Vs和动态门槛速度Vd之间时，摩擦系数在Vs~Vd和-Vs~Vd之间插值；当相对速度绝对值大于动态门槛速度时，采用动态摩擦系数。

1. 2机构的刚柔耦合动力学模型

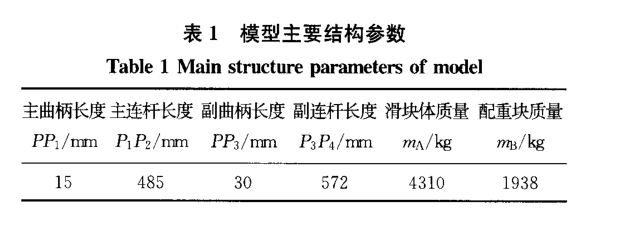
图3为JF75G-200高速压力机传动系统的结构简图，其传动系统的主要结构参数如表1所示。以图3中的P1点处的间隙为例，探讨间隙对振动的影响。Ft为压力机在冲裁工况下滑块所受的冲裁力。基于上述的间隙碰撞模型，建立高速精密压力机机构的动力学模型。

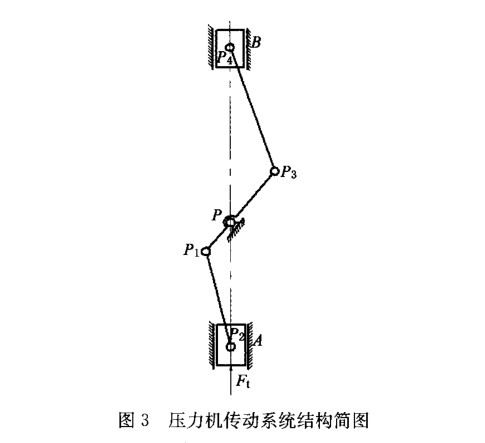
在Solidworks中建立高速压力机传动系统的三维模型，并将其导人Recurl)yn中，并利用其丰富的载荷和运动约束，创建构件间的约束。如图3

所示，曲柄P作为驱动原动件，周期为0 · 2 s；连杆滑块P2、曲轴副连杆P3、副连杆配重块P4约束副均为旋转副，曲轴连杆PI为间隙运动副；

采用Recurl)yn中FFlex功能对连杆进行网格划分，并设置好材料属性朗；压力机的工作载荷Ft为周期载荷，将其近似看做脉冲冲击载荷“，使用

IF与STEP 函数定义。图4为高速精密压力机传动系统的刚柔耦合动力学模型。

根据压力机相关部件材料特性 ，用式 (3) 算得P 点处间隙刚度，具体参数如表 2 所示。

2间隙对高速压力机振动的影响

引起压力机振动的激振力的来源主要有两个方面：一是曲柄滑块的回转部件和往复运动部件没有达到理想的动平衡，主要包括曲轴和飞轮、曲柄滑块机构的不平衡；另一个则是冲压过程的冲击力引起的振动，其相当于瞬时间上模给下模施加一个冲量。在压力机工作中，振动的大小与压力机的刚度和综合间隙有关，压力机的刚度大，各连接、运动部件的综合间隙小，则振动小。下面分别探讨间隙对这两种振动的影响。

2· 1间隙对不平衡惯性力引起的振动的影响

一般来说，高速压力机的振动是由激振力的大小决定的，激振力主要为曲柄滑块机构的惯性力。该惯性力通过作用机身，使机器和支撑机器的地面产生振动“。

为了分析间隙对不平衡惯性力引起振动的影响，对300次· min一1转速，无间隙和间隙为0 · 05 mm 两种情况分别进行仿真分析，得到压力机惯性力的变化曲线如图5a所示。比较两条曲线可知，无间隙的理想约束副与0 · 05 mm的间隙接触碰撞模型两种情况的惯性力变化趋势一致，但后者在上死点位置和下死点位置附近有很剧烈的波动，存在许多波峰，而且幅值也有所增大。

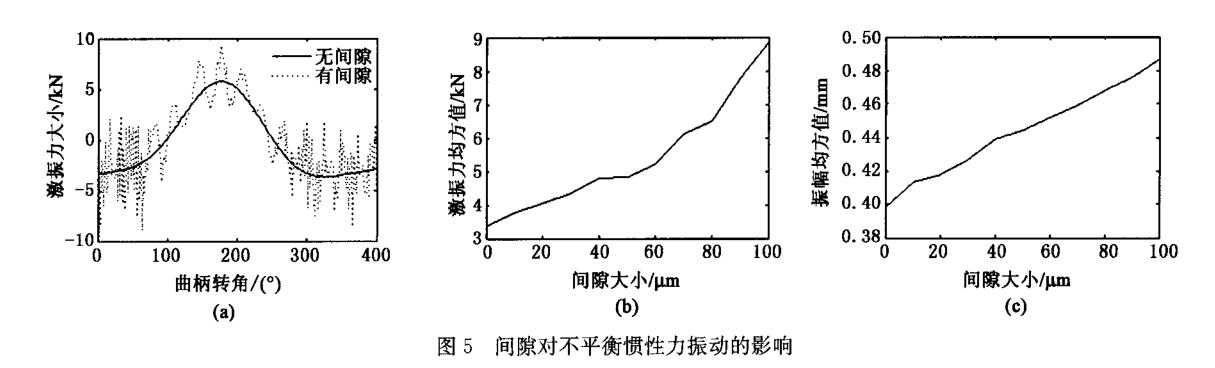
用惯性力的均方值来描述惯性力的大小，来比较不同间隙情况下惯性力波动的剧烈程度，通过多次仿真结果分析，得到无间隙以及间隙为0 · 01、 0 · 1 mm下惯性力均方值的变化如图5b所示。可见，随着间隙的增加，惯性力的均方值也迅速增大，间隙为0 · 1 mm与无间隙时相比，惯性力均方值增大了164％，这意味着惯性力的波动也更加剧烈。

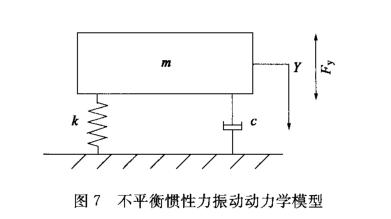
为了探讨惯性力的波动对机身振动的影响，通过RecurDyn中的Control功能与Matlab联合仿真，得到机身的振动曲线，具体步骤如图6所示。Simu link中计算压力机不平衡惯性力引起振动所用的动力学模型如图7所示，其中：为压力机的质量；差为隔振器刚度；c为隔振器阻尼；Fy为不平衡惯性力，其值由RecurDyn求解获得。压力机不平衡惯性力振动动力学参数如表3所示。

通过多次仿真结果分析 ，得到无 间隙以及间隙为 0．01～O．1 m m 下机身最大振幅的变化情况，如图 5c 所示。从 图中可以看出，间隙越大 ，机身振动越大，间隙为 0．1 m nl与无间隙时相比，最大振幅增大了22 。机身振幅随间隙近似呈线性增大，变化规律为：（5）

式中：y为机身振幅。

2．2 间隙对冲裁力引起的振动的影响

实际上激振力还包括上、下模具接触时 的打击力 ，其相当于瞬时间上模给下模施加一个冲量 ，即冲裁力 。

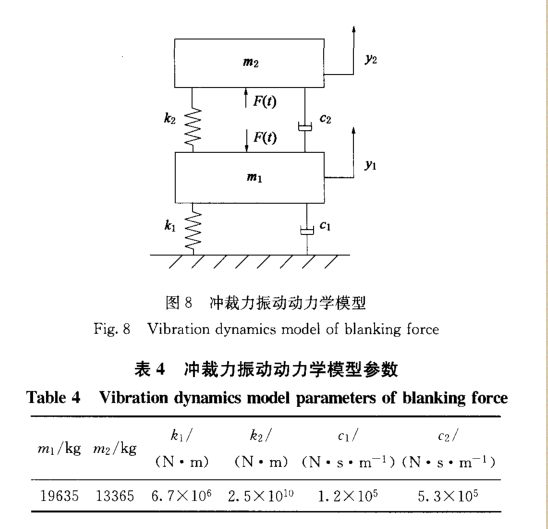
采用与不平衡惯性力同样的方法分析 间隙对冲裁力引起振动的影响。Sim ulink 中计算压力机 冲裁力引起振动所用的动力学模型如图 8 所示

，其中：m1为压力机下横梁的质量；k1为隔振器刚度；c1为隔振器阻尼；m2为压力机上横梁和立柱的质量；k2为压力机机身刚度；c2

为压力机结构阻尼；F (f)为冲裁力，其值由RecurDyn 求解获得 。压力机冲裁力振动动力学模型参数如表 4 所示。

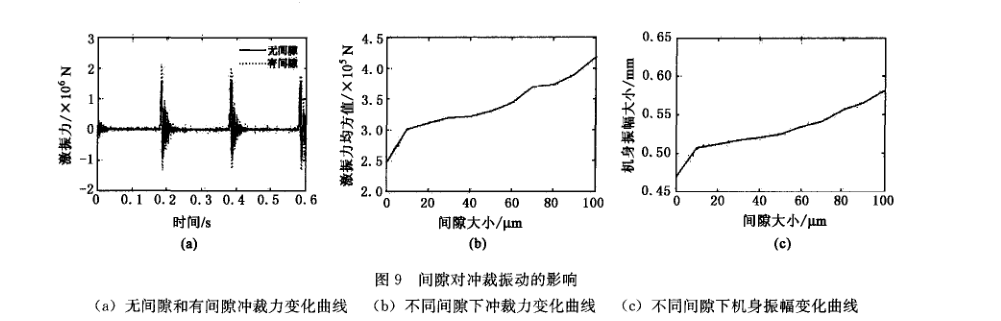
300次 。mln-l转速下，无间隙和间隙为 0 · 05 mm情况下，压力机冲裁力的变化曲线如图9a 所示，可以看出，无间隙的理想约束副与0

05 mm 的间隙接触碰撞模型两种情况激振力的变化趋势一致，但是后者的幅值更大。通过多次仿真结果分析，得到无间隙以及间隙为0 ·

01、0 · 1 mm情况下，冲裁力均方值以及机身振幅的变化曲线分别如图9b、图9c所示。从图中可以看出，间隙越大，冲裁力均方值和机身振

动越大。间隙为0 · 1 mm与无间隙时相比，冲裁力均方值增大了70％，振幅增大了24 ‰。机身振幅随间隙变化分为两段，变化规律为：

3   结论

（1）      间隙的存在使得引起激振力相比无间隙情况下波动更明显，呈现出高频振荡的特点，而且相比理想情况的幅值更大。说明间隙的存在会

增大运动副之间碰撞力，产生脉冲式的接触碰撞力，使得曲轴所受到的激振力增大。

（2）      间隙增大，激振力的波动更加剧烈，机身的振幅也随之增大。间隙的大小对激振力和机身振幅都有较大影响。

（3）      考虑运动副间隙的压力机传动系统更加真实的反映了压力机传动系统的动力学特性，本文建立的含间隙曲柄滑块机构传动的刚柔耦合动

力学模型为压力机分析和机构设计提供了基础。